조합 항등식의 조합론적 증명
조합론은 수학의 한 분야로, 경우의 수와 확률, 그리고 배열의 수학적 원리를 탐구하는 학문입니다. 특히 조합 항등식은 조합론에서 중요한 도구로, 이를 통해 복잡한 수학적 관계를 간단하게 정리하고 증명할 수 있습니다. 하지만 많은 사람들이 조합 항등식의 증명을 복잡한 계산으로만 이해하려고 합니다. 이에 비해 조합론적 증명은 직관적이고, 상황을 시각적으로 이해할 수 있는 장점이 있습니다.
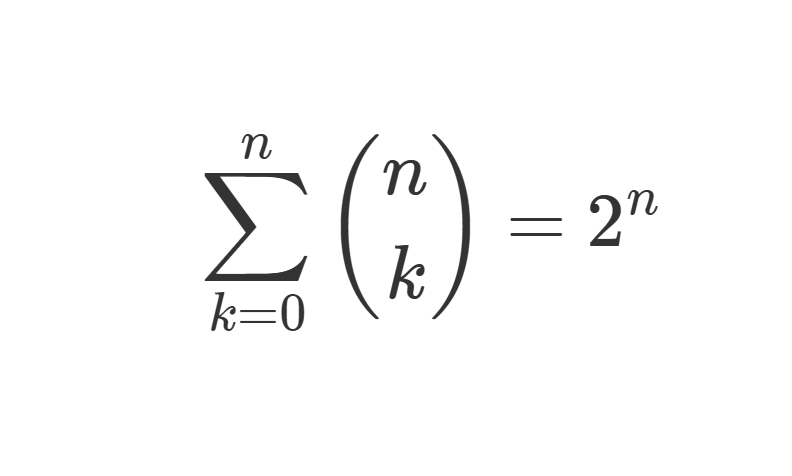
조합 항등식은 이항 계수와 관련이 깊으며, 복잡한 수학적 개념들을 단순한 상황으로 재구성하여 설명하는 데 유용합니다. 조합론적 증명은 특정 상황을 가정하고, 해당 상황에서 발생할 수 있는 경우의 수를 두 가지 다른 방식으로 계산하여 동일함을 입증하는 과정을 통해 성립합니다.
이번 글에서는 대표적인 조합 항등식 몇 가지를 선정하여, 이를 조합론적 관점에서 증명하는 과정을 살펴보겠습니다. 이러한 접근 방식을 통해 독자들이 조합 항등식의 본질을 좀 더 쉽게 이해할 수 있기를 바랍니다. 또한, 조합 항등식의 실제 응용 사례를 살펴보며, 그 유용성을 함께 탐구해 보겠습니다.
조합 항등식이란 무엇인가?
조합 항등식은 주어진 조건에서 경우의 수가 서로 동일하다는 사실을 보여주는 수학적 관계입니다. 예를 들어, $ \binom{n}{k} $와 같은 이항 계수는 특정한 조건에서의 경우의 수를 나타내며, 이를 조합 항등식을 통해 서로 연결할 수 있습니다.
조합 항등식의 일반적인 형태는 다음과 같습니다:
$$
\sum_{k=0}^{n} \binom{n}{k} = 2^n
$$
이 항등식은 $ n $개의 원소를 선택하는 모든 가능한 경우의 수가 $ 2^n $이라는 사실을 의미합니다. 이러한 항등식은 다양한 방법으로 증명될 수 있는데, 그중에서도 조합론적 증명은 특히 직관적이고 이해하기 쉽습니다.
조합론적 증명의 기본 원리
조합론적 증명은 수학적 관계를 단순히 계산을 통해 증명하는 대신, 문제를 특정한 상황으로 변환하여 그 관계를 설명합니다. 예를 들어, $ \binom{n}{k} $는 $ n $개의 원소 중에서 $ k $개의 원소를 선택하는 경우의 수를 나타냅니다. 이러한 의미를 시각적으로 이해하면, 항등식이 무엇을 의미하는지 명확히 알 수 있습니다.
조합론적 증명을 구성하는 데에는 다음과 같은 단계를 따릅니다:
- 상황 설정: 문제를 특정한 조합적 상황으로 변환합니다.
- 경우의 수 계산: 두 가지 다른 방법으로 경우의 수를 계산합니다.
- 결론 도출: 두 계산 결과가 동일함을 보여줍니다.
조합론적 증명은 단순히 결과를 도출하는 데 그치지 않고, 문제의 배경과 논리를 명확히 이해하도록 돕는 과정이기도 합니다. 이러한 접근 방식은 특히 복잡한 문제를 직관적으로 이해하고 설명하는 데 효과적입니다.
대표적인 조합 항등식과 증명
1. 이항 계수의 합 $ \sum_{k=0}^{n} \binom{n}{k} = 2^n $
상황 설정: $ n $개의 서로 다른 원소가 있는 집합에서 부분집합을 선택하는 경우를 생각합니다.
경우의 수 계산:
- $ n $개의 원소에서 부분집합을 선택하는 모든 경우의 수는 각 원소가 포함되거나 포함되지 않는 두 가지 경우로 나뉩니다. 따라서 총 경우의 수는 $ 2^n $입니다.
- $ k $개의 원소를 선택하는 경우의 수는 $ \binom{n}{k} $입니다. 이를 $ k = 0 $부터 $ n $까지 더하면 모든 부분집합을 포함하게 되므로 $ \sum_{k=0}^{n} \binom{n}{k} $가 됩니다.
결론: 두 경우의 수가 동일하므로 $ \sum_{k=0}^{n} \binom{n}{k} = 2^n $이 성립합니다.
이 증명은 직관적으로 이해하기 쉽고, 조합론의 기본 원리를 잘 보여주는 사례입니다. 이를 통해 이항 계수와 집합의 관계를 더욱 명확히 알 수 있습니다.
2. 파스칼의 삼각형 항등식 $ \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k} $
상황 설정: $ n $개의 원소 중에서 $ k $개의 원소를 선택하는 경우를 생각합니다.
경우의 수 계산:
- 첫 번째 원소를 포함하는 경우: $ n-1 $개의 원소 중 $ k-1 $개를 선택하는 경우로 $ \binom{n-1}{k-1} $입니다.
- 첫 번째 원소를 포함하지 않는 경우: $ n-1 $개의 원소 중 $ k $개를 선택하는 경우로 $ \binom{n-1}{k} $입니다.
결론: 두 경우를 더하면 전체 경우의 수가 되므로 $ \binom{n}{k} = \binom{n-1}{k-1} + \binom{n-1}{k} $가 성립합니다.
파스칼의 삼각형은 조합론의 기초로, 이항 계수를 효율적으로 계산할 수 있는 도구입니다. 이 항등식은 동적 프로그래밍에도 중요한 기반을 제공합니다.
3. 멀티셋 분할 항등식 $ \binom{n+k-1}{k} $
상황 설정: $ n $개의 사탕을 $ k $명의 아이들에게 나누는 경우를 생각합니다. 이때, 한 아이가 여러 개의 사탕을 받을 수 있습니다.
경우의 수 계산:
- $ n $개의 사탕과 $ k-1 $개의 구분선을 배열하는 문제로 변환합니다.
- 배열 가능한 모든 조합의 수는 $ \binom{n+k-1}{k} $로 계산됩니다.
결론: 멀티셋 문제는 조합론적 증명을 통해 간단히 해결할 수 있으며, 이는 다양한 실생활 문제에도 응용될 수 있습니다.
조합론적 증명의 응용
조합론적 증명은 단순한 이항 계수의 항등식에서 끝나지 않습니다. 복잡한 조합 문제, 확률론, 그래프 이론 등 다양한 분야에서 응용됩니다. 예를 들어, 그래프의 경로를 계산하거나 분할 문제를 해결하는 데에도 이러한 방법이 사용됩니다.
그래프 이론에서의 응용
그래프 이론에서 조합론적 항등식은 경로 계산, 최소 신장 트리, 네트워크 플로우 문제 등 다양한 응용을 가집니다. 조합론적 증명을 통해 그래프의 구조적 특성을 보다 명확히 이해할 수 있습니다.
동적 프로그래밍과의 연계
동적 프로그래밍에서 조합론적 항등식은 알고리즘을 설계하는 데 중요한 역할을 합니다. 예를 들어, 파스칼의 삼각형은 이항 계수를 계산하는 기본 알고리즘으로 활용됩니다. 이를 통해 복잡한 문제를 효율적으로 해결할 수 있습니다.
결론
조합 항등식은 수학의 다양한 분야에서 중요한 도구로 사용되며, 이를 이해하고 증명하는 과정은 조합론의 핵심 중 하나입니다. 특히 조합론적 증명은 직관적이고 시각적인 접근 방식을 제공하여 복잡한 문제를 간단하게 풀 수 있도록 돕습니다.
이번 글에서는 대표적인 조합 항등식 몇 가지를 소개하고, 이를 조합론적 관점에서 증명하는 과정을 살펴보았습니다. 이를 통해 조합론의 매력을 느끼고, 다양한 문제 해결 능력을 키울 수 있기를 바랍니다. 나아가, 이러한 증명 방식을 실제 문제 해결에 응용하는 방법도 탐구해 보길 추천합니다.
'과학 - 수학 물리 생물' 카테고리의 다른 글
| 말려 먹으면 좋은 식품들 (0) | 2025.01.04 |
|---|---|
| 뉴턴의 1~3법칙, 관성의법칙, 가속도의법칙, 작용과 반작용의 법칙 (0) | 2025.01.03 |
| 벌꿀 먹는 법, 좋은 진짜 벌꿀 구별법 (0) | 2025.01.02 |
| 초고속별 항성(Hypervelocity Star, HVS) 'CWISE J1249+3621' (0) | 2025.01.02 |
| 등차수열의 합 공식 (0) | 2025.01.02 |



