이등변 삼각형 넓이 공식 구하기

이등변 삼각형 넓이 공식 구하기

이등변 삼각형은 두 변의 길이가 같은 삼각형으로, 그 독특한 대칭성과 구조 덕분에 다양한 분야에서 활용되고 있습니다. 수학 문제를 풀거나 실제 생활에서 측정 작업을 할 때, 이등변 삼각형의 넓이를 정확히 구하는 것은 매우 중요합니다. 그렇다면 이등변 삼각형의 넓이를 어떻게 효율적으로 구할 수 있을까요? 이번 포스팅에서는 이등변 삼각형의 넓이를 구하는 다양한 공식을 소개하고, 이 공식을 이해하고 활용하는 데 도움이 될 만한 내용을 알아보겠습니다.

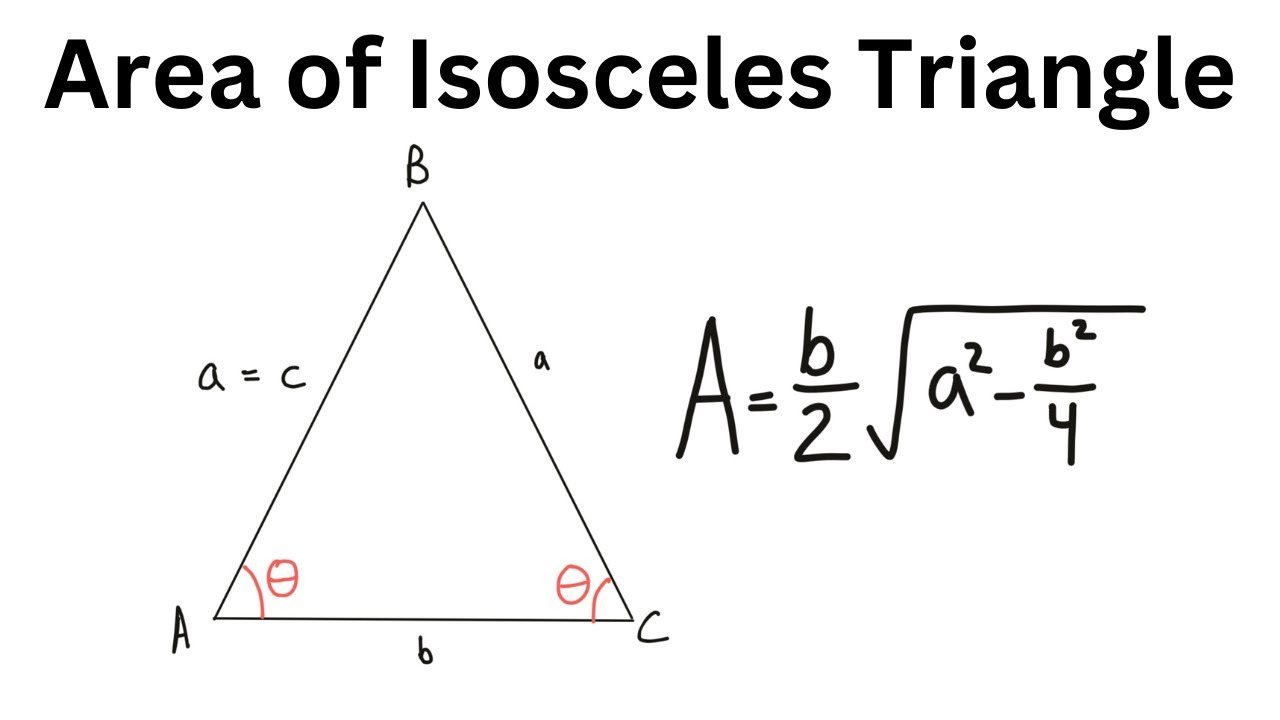
넓이 공식은 그저 하나의 숫자를 도출하는 데 그치는 것이 아닙니다. 이 공식은 수학적 개념의 확장을 통해 이등변 삼각형의 다양한 성질을 이해하게 도와주며, 이를 활용한 문제 풀이 능력을 향상시킬 수 있습니다. 오늘은 이등변 삼각형의 넓이 공식을 보다 쉽게 이해하고 적용할 수 있도록 다양한 예시와 설명을 곁들여 여러분과 함께 공부해 보겠습니다.

이등변 삼각형의 넓이를 구하는 방법을 잘 익혀 두면 수학 시험에서나 실생활에서 유용하게 사용할 수 있습니다. 예를 들어, 건축 현장에서 삼각형 형태의 구조물을 설계할 때, 혹은 정원에서 삼각형 모양의 공간을 디자인할 때 이등변 삼각형의 넓이를 계산하는 것은 필수적입니다. 이러한 상황에서 정확한 넓이를 구하기 위해서는 공식을 이해하고, 어떻게 적용해야 할지 아는 것이 중요합니다. 이번 글에서는 이등변 삼각형의 넓이를 계산하는 다양한 방법과 그 활용 사례들을 좀 더 깊이 있게 다뤄보겠습니다.

이등변 삼각형 넓이 공식

이등변 삼각형의 넓이를 구하는 공식은 크게 두 가지 형태로 나뉠 수 있습니다. 첫 번째는 기초적인 삼각형 넓이 공식을 사용하는 방법이고, 두 번째는 삼각함수를 활용한 공식을 사용하는 방법입니다. 이를 통해 다양한 상황에서 이등변 삼각형의 넓이를 구할 수 있습니다.

1. 기본 넓이 공식

가장 기본적인 넓이 공식을 사용하여 이등변 삼각형의 넓이를 구하는 방법을 알아보겠습니다. 모든 삼각형의 넓이는 다음 공식을 통해 구할 수 있습니다.

넓이 = (밑변 × 높이) / 2

이등변 삼각형의 경우, 두 변의 길이가 동일하므로 높이를 찾는 과정이 중요합니다. 이등변 삼각형은 두 변의 길이가 같기 때문에, 밑변의 중점에서 정점까지 수직으로 내린 선이 높이가 됩니다. 이를 통해 넓이를 쉽게 계산할 수 있습니다.

예를 들어, 밑변의 길이가 8cm이고 높이가 6cm인 이등변 삼각형이 있다고 가정해봅시다. 이 삼각형의 넓이는 다음과 같이 구할 수 있습니다.

넓이 = (8 × 6) / 2 = 24 cm²

이처럼 밑변과 높이가 주어진 경우에는 간단한 계산으로 넓이를 구할 수 있습니다. 이 방법은 매우 직관적이며, 시각적으로도 쉽게 이해할 수 있는 방법입니다.

하지만 때때로 높이가 직접적으로 주어지지 않는 경우가 있습니다. 이러한 상황에서는 피타고라스의 정리를 활용해 높이를 계산한 후 넓이를 구해야 합니다. 예를 들어, 밑변의 길이가 10cm이고 두 변의 길이가 각각 13cm인 이등변 삼각형의 경우, 높이는 피타고라스 정리를 통해 구할 수 있습니다. 이와 같은 과정을 통해 복잡한 형태의 이등변 삼각형의 넓이도 쉽게 계산할 수 있습니다.

2. 삼각함수를 이용한 넓이 공식

이등변 삼각형의 넓이를 구할 때, 삼각함수를 활용하는 방법도 있습니다. 만약 밑변의 길이와 함께 밑변에 대한 각도를 알고 있다면, 삼각함수를 이용해 넓이를 계산할 수 있습니다. 이를 위해서는 사인 함수(sin)를 활용하는 공식이 유용합니다.

넓이 = 1/2 × a × b × sin(θ)

여기서 a와 b는 두 변의 길이이며, θ는 그 두 변 사이의 각도입니다. 이등변 삼각형에서는 두 변의 길이가 같으므로, 이 공식을 다음과 같이 단순화할 수 있습니다.

넓이 = a² × sin(θ) / 2

예를 들어, 두 변의 길이가 10cm이고, 그 사이의 각도가 45도인 이등변 삼각형의 넓이를 구한다고 가정해봅시다. 이 경우 넓이는 다음과 같이 계산됩니다.

넓이 = (10² × sin(45°)) / 2 = 50 × √2 / 2 = 35.36 cm² (약)

삼각함수를 사용하면 각도에 따라 넓이를 구할 수 있어, 다양한 형태의 이등변 삼각형에 대응할 수 있습니다. 이 방법은 특히 각도가 주어진 경우 매우 유용하며, 삼각형의 형태가 조금 더 복잡할 때도 적용할 수 있는 강력한 도구입니다.

이러한 삼각함수를 이용한 넓이 계산은 트리곤메트리의 기본적인 개념을 이해하는 데에도 도움이 됩니다. 예를 들어, 사인 함수의 성질을 이해하고 이를 실제 문제에 적용하는 과정을 통해 삼각형의 넓이뿐만 아니라 삼각함수의 활용성도 익힐 수 있습니다.

이등변 삼각형의 성질과 활용

이등변 삼각형은 그 독특한 성질 덕분에 여러 수학적 문제와 실제 상황에서 활용됩니다. 특히 그 대칭성은 다양한 문제를 쉽게 해결하는 데 도움을 줍니다. 이등변 삼각형의 성질을 이해하면 넓이 공식을 더 쉽게 이해하고 활용할 수 있습니다.

1. 대칭성

이등변 삼각형은 대칭 축을 가지고 있습니다. 이 대칭 축은 밑변의 중점에서 정점까지 이어진 선으로, 이 선은 삼각형을 두 개의 같은 크기의 직각삼각형으로 나눕니다. 이 성질을 이용하면 삼각형의 넓이를 구할 때 높이를 쉽게 찾을 수 있습니다.

대칭성은 이등변 삼각형의 구조적 안정성을 제공하는 중요한 요소입니다. 예를 들어, 건축물이나 다리의 설계에서는 이 대칭성을 이용해 안정적인 구조를 구현할 수 있습니다. 대칭이 주는 시각적인 아름다움도 무시할 수 없으며, 많은 예술 작품에서도 이등변 삼각형의 대칭성이 활용됩니다.

2. 삼각형의 내각

이등변 삼각형의 두 밑각은 항상 같습니다. 이 성질은 삼각형의 각도를 이용해 넓이를 구하는 문제에서 유용하게 쓰입니다. 예를 들어, 각도가 주어진 경우 나머지 각도를 쉽게 계산할 수 있으며, 이를 통해 삼각형의 다른 성질을 파악할 수 있습니다.

이등변 삼각형의 내각은 삼각형의 형태를 이해하는 데 중요한 역할을 합니다. 두 밑각이 동일하다는 것은 삼각형이 얼마나 대칭적인지를 보여주며, 이를 통해 삼각형의 형태를 쉽게 예측할 수 있습니다. 또한, 각도를 이용한 넓이 계산에서 이 성질은 매우 유용하게 활용됩니다.

3. 실제 활용 예시

이등변 삼각형은 건축, 디자인, 그리고 자연 속에서도 자주 나타나는 형태입니다. 예를 들어, 다리의 구조나 건물의 외형에서 이등변 삼각형의 대칭성과 안정성을 활용하는 경우가 많습니다. 이러한 구조적 특징을 이해하면 이등변 삼각형의 넓이를 구하는 것이 단순한 계산을 넘어 실생활에 어떻게 적용될 수 있는지 알 수 있습니다.

자연 속에서도 이등변 삼각형은 흔히 발견됩니다. 나뭇가지의 배열이나 산의 경사면 등에서 이등변 삼각형의 형태를 볼 수 있습니다. 이러한 자연 현상을 이해하면, 우리가 살아가는 세상이 수학적 원리에 따라 움직인다는 것을 실감하게 됩니다. 또한, 이러한 형태를 모방하여 인간이 설계하는 많은 구조물들이 안정성을 확보하고 있는 것을 볼 수 있습니다.

건축물에서는 특히 삼각형의 형태가 중요한데, 이등변 삼각형의 대칭성과 안정성은 구조물의 내구성을 높이는 데 중요한 역할을 합니다. 교량, 탑, 그리고 다양한 건축 구조물에서 이등변 삼각형의 형태를 쉽게 찾을 수 있으며, 이는 안정적인 힘의 분산을 가능하게 합니다.

결론

이등변 삼각형의 넓이를 구하는 것은 기본적인 수학적 개념이지만, 이를 다양한 상황에서 활용할 수 있다는 점에서 매우 유용합니다. 기본 넓이 공식인 (밑변 × 높이) / 2부터 삼각함수를 활용한 공식까지, 상황에 따라 적절한 방법을 선택하여 넓이를 계산할 수 있습니다. 이등변 삼각형의 대칭성과 내각의 특성을 이해하면 넓이를 구하는 문제뿐만 아니라 다양한 수학적 문제도 더욱 쉽게 접근할 수 있습니다.

수학은 단순히 숫자를 계산하는 것을 넘어, 그 속에 숨겨진 패턴과 성질을 이해하는 학문입니다. 이등변 삼각형의 넓이를 구하는 공식을 통해 이러한 수학적 아름다움을 발견하고, 더 나아가 이를 실제 문제에 적용해 보는 것은 매우 뜻깊은 경험이 될 것입니다.

이등변 삼각형의 넓이를 구하는 과정은 수학적 사고력을 기르는 데 큰 도움이 됩니다. 단순한 공식을 외우는 것을 넘어서, 그 공식을 유도하고 실제 상황에 적용해 보는 것은 수학적 사고를 더욱 깊게 만들어 줍니다. 또한, 이를 통해 우리는 수학이 단지 학문적 지식에 그치는 것이 아니라, 실제 생활 속에서 어떻게 쓰일 수 있는지 경험하게 됩니다.

다양한 공식을 이해하고 그 활용 방법을 익혀 두면, 수학적 문제 해결 능력이 크게 향상될 것입니다. 이등변 삼각형뿐만 아니라 다른 기하학적 도형의 넓이와 성질도 이해하게 되면서, 수학적 사고의 폭을 넓혀 나갈 수 있습니다. 이번 기회를 통해 이등변 삼각형의 넓이 계산법을 완벽히 익히고, 다양한 문제에 적용해 보시기 바랍니다.